Критерий Стьюдента Программа
Теоретические сведения Метод Стьюдента применяется для сравнения двух выборок, взятых из одной и той же генеральной совокупности, или двух различных состояний одной и той же выборочной совокупности. При этом могут представиться следующие случаи: 1. По объему: 2.
T-критерий Стьюдента для независимых выборок применяется для сравнения средних значений двух независимых между собой выборок. Условия применения: Сравниваемые значения не составляют пару коррелирующих значений; Распределение признаков в каждой выборке соответствует. Критерий Стьюдента направлен на оценку различий величин средний значений двух выборок, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных. Основные статистики и t-критерий Стьюдента. Описательные статистики. Диалог Основные статистики и таблицы. В ходе рассмотрения примера мы будем использовать вымышленные сведения, чтобы читатель мог провести необходимые преобразования самостоятельно. Так, допустим, в ходе. Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок).
А) обе группы большие (n30); б) обе группы малые; в) одна — большая, вторая — малая. По составу: а) группы с попарно-зависимыми вариантами, когда i-тая варианта первой группы сравнивается с i-той вариантой второй группы; б) группы с попарно-независимыми вариантами (можно менять варианты местами внутри группы). Исходя из таких условий задачи могут быть трех типов: I. Сравнение двух больших (или одной большой, одной малой) групп с попарно-независимыми вариантами проводится по формулам: (1), (2), где: k — число степеней свободы, — объем первой выборки, — объем второй выборки, — среднее арифметическое 1 группы, — среднее арифметическое 2 группы, — ошибка репрезентативности 1 группы, — ошибка репрезентативности 2 группы. — критерий Стьюдента, по найденному значению которого определяют доверительную вероятность различия групп. Сравнение двух малых групп с попарно-независимыми вариантами проводится по формулам: (3) где обозначения букв те же, что и в первом случае. Сравнение двух малых групп с попарно-зависимыми вариантами.
(7) Пример 7.1. По числу подтягиваний две группы показали следующие результаты: = 10,0 = 35 = ±1,3 = 14,5 = 40 = ±1,5 Определить достоверность различия этих групп по средним арифметическим. Решение: Задача на первый случай, так как группы по объему большие и варианты попарно-независимы. Следовательно, решать нужно по формулам:,., k = 35 + 40 - 2 = 73.
Критерий Фишера
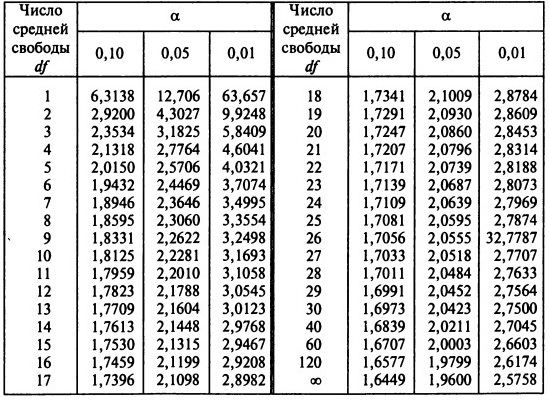
По таблице t-критиериев Стьюдента определим доверительную вероятность: 0,95. Приведенная рабочая форма применяется и в I случае, если выборки даны своими вариантами, а, и — неизвестны. До начала и после подготовительного этапа тренировочного цикла в команде баскетболистов фиксировалась результативность выполнения бросков в%. Определить значимость различных состояний команды. Решение: Задача на третий случай, так как сравниваются два различных состояния одной и той же выборки.
Решать следует по формулам (5), (6) или (5), (7). Данные занесем в рабочую таблицу вида: По таблице t-критериев определим, что различие достоверно (причем, ) по II порогу доверительной вероятности. Команда баскетболистов в результате проведенного цикла тренировок показала результаты значительно выше прежних. Значимость определяется по формуле. Определить различия в скоростно-силовой подготовке студентов-спринтеров, если их результаты в тройном прыжке таковы: Решение: 1. Рабочая гипотеза: т.к., то предположим, что спортсмены группы Х имеют более высокий уровень развития скоростно-силовых качеств, чем спортсмены группы Y.
Критерий Стьюдента Таблица
Подтвердим данное предположение, рассчитав t -критерий Стьюдента по формуле: = Вывод: ЗАДАЧА 2. Сравнить какая группа студентов по показателю ЧСС покоя лучше, если их результаты таковы ( — данные 1-ой группы, — данные 2-ой группы): Решение: 1. Результаты тестирования занести в рабочую таблицу и выполнить соответствующие расчеты: 2. На основании сравнения средних значений показателей X и Y выдвинуть рабочую гипотезу: 3. Подтвердить выдвинутое предположение, рассчитав значение t -критерия Стьюдента и числа степеней свободы по формулам: Вывод: ЗАДАЧА 3. Определить значимость различий показателей количества подтягиваний на перекладине в группе спортсменов до начала и в конце периода тренировок силового характера, если данные таковы: В начале периода В конце периода Решение: 1.
Занести результаты тестирования в рабочую таблицу и сделать соответствующие расчеты: 2. Рассчитать значения t -критерия Стьюдента и числа степеней свободы по формулам: Вывод. Контрольные вопросы 1.Цель применения метода Стьюдента. 2.Доверительная вероятность и уровень значимости по Стьюденту, их пороги. 3.Какие выборки называются попарно-зависимыми? 4.Какие выборки называются попарно-независимыми? © 2012 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования 'Кубанский государственный университет физической культуры, спорта и туризма' Адрес: 350015, г.Краснодар, ул.Буденного, 161 Телефон: (8612) 55-35-17, факс: (8612) 55-35-73 E-mail.